Building an ARMA or ARIMA time series model

 

Well, Nowadays it is quite common to use time series data to analyze or forecast the future value of the given variables (commonly such models used for forecasting the FX rate ) So let me share what I know about building such models.

As suggested in the Box-Jenkins Methodology in 1976, it is common to follow essential stages to build an ARMA, (it goes same with the ARIMA models) models. There are three essential stages including :

1. Identification
2. Estimation
3.Diagnostic and Checking

1. In identification stage, stationarity is very essential and really important.

The first step is always to check stationarity for the underlying series. But, before rush into that, you should look for outliers, trends and seasonal components in your time series data. Such outliers, trends and seasonal components have negative effect on the quality of the forecast as well as estimation of analysis. Also they hide some important features of time series. So if there are some observable outliers then you have to remove it before checking the stationarity for the underlying series.

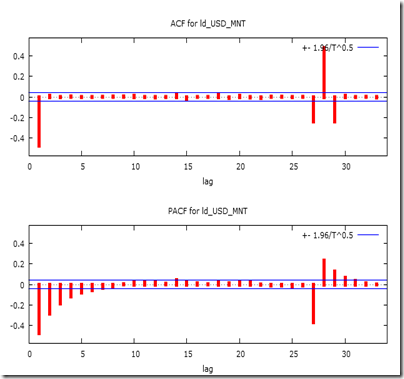
As for the stationarity, a brief idea can be obtained by looking at the time series graph (sometimes called time series plot) and correlogram. For instance, time series graph could show you some deterministic trends which suggesting non-stationarity. Moreover, if correlogram has a few significant spikes at very small lags, and cuts off drastically or dies down quickly then it shows in time series. Otherwise, it is non-stationary.

 

 

To be sure, Augmented Dickey Fuller (ADF) test can be used to identify the stationarity of the time series. From the result of ADF test, we might get non-stationary time series data. In that case, we can use first difference, seasonal difference or natural logarithm difference to make it stationary.  (There are many other ways to make the non-stationary time series data into stationary )

Once you got the stationary form of the time series, then you have to look at the autocorrelation function and partial autocorrelation function to determine possible numbers for orders of ARMA(p,q) model.

2. From identification stage, it may not lead to single model, hence you have to examine several models. The main approach for fitted Box-Jenkins models are non-linear least squares and most preferably, maximum likelihood estimation.

3. Diagnostic and Checking

In this stage, you must check whether residuals are white noise or not. Unless residuals are white noise, model is not fitted and can’t be used to forecast the future value. So, after eliminating several models, you may still get a few good fitted models. So the question is how to choose the best model among the chosen ones. Now, we use Akaike information criterion or Schwarz information criterion to decide which one is the most accurate and can be used for forecasting.

 

Personally, I use Eviews and Gretl (quite good and 100% free software, download from here)